Eléments de logique Combinatoire

Théorie
La logique combinatoire est utilisée comme base pour la conception de langages de programmation fonctionnels. Elle répond à un modèle théorique de calcul. L’information traitée est de type binaire. Elle est représentée par des signaux électriques à 2 états {0; 1}.

Une fonction logique définit l’état de variables de sortie en fonction de la combinaison de variables d’entrée, sans que la notion de temps n’intervienne. L’état des sorties n’est régi que par les états des variables d’entrée. Pour les différentes variables :

• Variables d’entrée : il s’agit de signaux provenant d’autres systèmes ou d’organes de commande, tels que des boutons poussoir, des interrupteurs, des capteurs, identifiés ou connus a priori.

• Variables de sortie : il s’agit d’un signal permettant l’activation ou non d’un système à commander, comme des voyants, des lampes, des moteurs.

De manière plus générale, la logique combinatoire permet la réalisation de fonctions logiques de type UAL (Unité arithmétique et logique), des transcodeurs, des afficheurs 7 segments, etc.

Il y a 3 fonctions logiques élémentaires à connaître qui permettent d’exprimer toutes fonctions logiques. Afin d’exprimer leur fonctionnalité, nous utilisons des tables de vérité. Une table de vérité est une table mathématique permettant de représenter de manière sémantique des expressions logiques, et de spécifier leur valeur pour chaque combinaison des entrées.

Fonctions élémentaires

• La fonction logique NON

  Soit la variable binaire x. La sortie S de la fonction logique NON est spécifiée dans la table de vérité suivante :

  

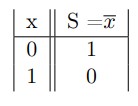
• La fonction logique ET
  Considérons deux variables binaires x et y. La sortie S de la fonction logique ET est spécifiée dans la table de vérité suivante :

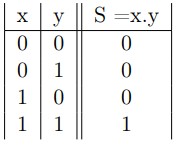
`.’ est l’opérateur ET (AND) qui est différent de l’opérateur mathématique `.’,  la multiplication en arithmétique.

• La fonction logique OU
  Considérons deux variables binaires x et y. La sortie S de la fonction logique OU est spécifiée dans la table de vérité suivante :

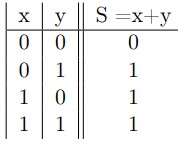
`+’ est l’opérateur OU (OR) qui est différent de l’opérateur `+’,  l’addition en arithmétique.

Autres fonctions logiques

• La fonction logique NON ET
  Considérons deux variables binaires x et y. La sortie S de la fonction logique NON ET est spécifiée dans la table de vérité suivante :

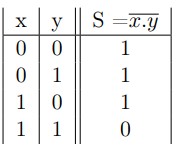
• La fonction logique NON OU
  Considérons deux variables binaires x et y. La sortie S de la fonction logique NON OU est spécifiée dans la table de vérité suivante :

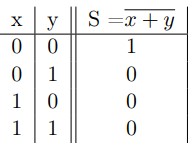
• La fonction logique OU Exclusif
  Considérons deux variables binaires x et y. La sortie S de la fonction logique OU Exclusif est spécifiée dans la table de vérité suivante :

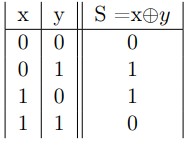
• La fonction logique ET Exclusif
  Considérons deux variables binaires x et y. La sortie S de la fonction logique ET Exclusif est spécifiée dans la table de vérité suivante :

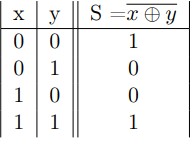
Fonctions logiques

Les fonctions logiques à programmer sont souvent plus complexes. Elles peuvent être régies par plus de 2 variables d’entrée. La démarche est cependant la même. Il est nécessaire de dresser leur table de vérité, puis de simplifier les expressions obtenues à l’aide de l’algèbre de Boole ou de tableaux de Karnaugh.

Un exemple d’une fonction logique est donnée ci-dessous :

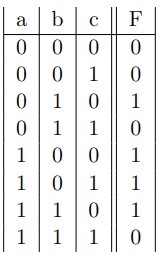 La fonction F est exprimée à partir de l’ensemble des combinaisons d’entrées conduisant à son activation. Soit : 

La fonction peut être programmée en l’état, mais une version simplifiée permet de faciliter sa programmation. Pour cela nous pouvons utiliser l’algèbre de Boole, ou un tableau de Karnaugh.

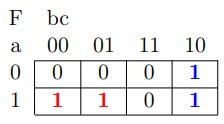
Deux regroupements de 2 sont possibles, celui des `1‘ en rouge et le second en bleu, conduisant à l’expression simplifiée :